“Unit symbols are mathematical entities and not abbreviations.”
The International System of Units 9th Edition, 2022, Pg.147
As a teacher with 10 years of A Level Mathematics and Further Maths teaching under my belt, sometimes the simplest and most used concepts, the concepts that students themselves feel confident that they ‘know’, are where you notice a lack of depth in their understanding, which then holds back progress elsewhere. One such area where I have found this is with units of measure.
Fuelled by observations and questions of students, discussions with peers at my institution and beyond, have led to me looking to investigate a conjecture further – is the way we introduce and then reinforce the use and meaning behind units of measure not supporting students to realise the units themselves are mathematical entities, not simply an abbreviation or label?
In some ways this perception can be traced to the exam years and focus that students naturally go through during those periods – not directly an indictment of how teaching of a concept was structured and delivered. Below are common exam paper formats of how final answers are expected to be presented across Maths and Science papers from AQA.

If this is how the majority of calculation questions appear for students, is it a surprise that they often view units as a ‘label’ and afterthought? They do mathematical working devoid of units, and then when presenting the solution they often don’t need to think about the units. Even when units aren’t provided for the student, they are generally something tagged on at the end of the question, and unless a conversion is required, often not thought about until that point of providing the label at the end.
How are we to encourage young people to see unit symbols as mathematical entities when curriculum, syllabus, assessment and therefore general teaching methods are designed such that they rarely, if ever, actually ‘do mathematics’ on these values?
What might be the benefits of doing things differently?
Square and Cubic _______metres
As I have referenced SI unit information at the beginning, I think it would be amiss not to discuss where I personally fall foul of the correct verbalisation of measure – and a very quick straw poll of colleagues in person, and peers across maths, science and primary education on Threads suggests I am not the only one. I am talking about m2 and m3 – often verbalised as “metres squared” and “metres cubed” – as seen below.

The correct verbalisation of these units, as per the International System of Units are ‘square metres’ and ‘cubic metres’. The documentation even goes into detail as to how the oft verbalised “metres squared” and “metres cubed”, by both myself and others, is incorrect and not the standard. This is to avoid linguistic ambiguity, as “6 square metres” has one clear meaning; however depending on stress, pause and emphasis “six…metres squared” and “six metres…squared” can have two dramatically different mathematical interpretations.

I am therefore aware of myself as a hypocrite. I am going to be on my ‘high horse’ of discussing approaches of teaching a key principle relating to SI units – whilst myself am guilty of a different error of a similar type elsewhere. Possibly worse, as instead of error of oversight or omission, it’s using what is explicitly deemed incorrect terminology.
However, as stated I am not alone in this, one conjecture for reason is that given our nature as educators our verbalisation of the units often comes at the end of a modelled calculation. As we write the 6, we write the m, and then we write the power of 2 it encourages us to accompany this by saying “six…metres…squared” to emphasise the elements of our writing.
This error however can be turned to a positive regarding the interpretation and application of units of measure as mathematical entities, not merely labels and abbreviations of the words. Approaching m2 as an extension of 32 or an algebraic x2, it is a measurement in metres multiplied by another measurement in metres. Students can often recite the first part, but it’s the link to the idea that this means you literally multiply metres by metres which is often lacking.
How do we introduce square and cubic units – how is the knowledge reinforced?
Basic units of measurement such as metres, square metres and cubic metres are introduced within primary education. This underpinning to algebra is therefore not appropriate in the early stages of delivery, particularly with curriculum structured as it currently is. Instead, physical and geometric representations of shapes are used in order to illustrate concepts of area and volume. The ‘square centimetres’ due to a literal ‘square’, a ‘cubic centimetres’ due to a literal ‘cube’. The emphasis of a unit label as allowing ‘consistency’ between individuals, and the fact you have 2 or 3 dimensions of m or cm.
Even during A level post-16 provision I will often get a poorly constructed circular logic argument when discussing basic units – “Why is it square metres?/metres squared?” will often be responded with “As it is area”. This response however could easily be interpreted as ‘enough’ throughout their schooling – particularly when viewing things through the lens of the GCSE curriculum. It can appear as though the student has ‘fixed knowledge’ – they know area is m2, is there any reason to introduce more difficult conceptualisation, they ‘know it’?
Viewing the materials made available from Oak National Academy, both square numbers and area are elements of the year 5 key stage 2 syllabus. There are links with regards physical literal squares when discussing square numbers – which has long such been a convention, however this doesn’t particularly reciprocate into an approach of units2. Looking further into the key stage 3/key stage 4 resources you don’t get conceptual development in this area, it is as previously discussed treat as ‘fixed knowledge’ for the student – “for area you label…”. Three examples are provided below;



1) This is from a video introducing formal area. Here the notation is essentially that of a shorthand, merely a label. This is a video targeting some of the youngest students tackling this concept, so I understand that approach – it’s geometric logic. However the ‘units’ on the diagram becoming ‘units2’ with a limited explanation beyond “squares” does get to me somewhat.
2) This video moves on from square grids, and brings the concepts forward but reinforces the circular logic that students often repeat. Again the underpinning is geometric, the unit is a label.
3) This final video is for older students, and is ‘so close’ to tying this all together – however the two highlighted statements are not developed as sequiturs – missing an opportunity to emphasise units of measure as ‘active mathematical objects’.
Whilst it would be incredibly rudimentary – this is beginning to highlight an area that is lacking from the mathematics curriculum – dimensional analysis. This is an area that I feel is essential for developing not only mathematicians of calibre, but future scientists. It’s a topic that also sits perfectly on the cusp of ‘practical real life mathematics’ and something that helps provide meaning within the abstract as well.
What is Dimensional Analysis?
In its most rudimentary form, dimensional analysis is investigating and identifying the component parts of units and tracking them through calculations performed. I am far from the first person to discuss the absence of this from the core mathematics – a blog from Jemma Sherwood from 2019 laments its absence from the curriculum (https://educationblog.oup.com/secondary/maths/exam-insights-gcse-maths). It allows students to start to investigate and comprehend ‘why must this formula produce area?’, ‘why is my solution to this calculation a speed?’, ‘why does it not make sense to add the solutions to these two calculations?’. It is meaning building when it comes to calculations.
I’m not going to say it has entirely disappeared – much used resource provider CorbettMaths still includes elements of dimensional analysis, and browsing YouTube you will find a a variety of videos of both general mathematics and wider Science contexts – and a number of teachers such as Jemma Sherwood will continue to deliver these on an ad-hoc basic as well. However, looking into the resources labelled and shared on TES it shows a huge disparity between the focus and availability of resources and therefore likely emphasis within the classroom.
| Topic search term | Number of resources on TES |
| Units of measure | 5,833 resources under maths and a further 1494 in Science |
| Area | Over 8000 resources in maths/geometry |
| Volume | Over 3000 resources in maths/geometry |
| Dimensional analysis | 59 resources under maths and a further 104 under Science |
At this time I posit for the maths teachers, when was the last time you did a calculation where you actually included the units within your working? When was the last time that you encouraged this of a student? This is a absolutely tiny change in approach that can help illustrate and the concept of units as mathematical artefacts, and not a label or written shorthand.

Looking at potential benefits
This singular, minimal change – that doesn’t need to be a permanent fixture of your methods – can open up levels of understanding in a cohort – and act as a bridging gap between the concepts of algebra and arithmetic, as well as offering reciprocal links between different areas of the mathematics curriculum.
The approach of splitting the component parts of the calculation for area (and other unit based calculations) is the equivalent process for the approach of undertaking calculations in standard form – allowing links between different areas of mathematics, and brings a more holistic approach to the rules and laws of mathematics – not simply a ‘this specific thing fixes this specific problem’. Both methods also interlink with ‘laws of indices’, particularly offering the opportunity to support with understanding of negative indices, as well as general algebraic methods.

Applying these methods to problems based around Pythagoras’ Theorem also reinforces methods of surds, with algebraic adaptation. Treating units in this way is one of the methods I use to support students at Level 3 who struggle to work with ‘algebraic surds’ – they understand how this would interact with Pythagoras’.

This unit relationship and appreciating how the units transform under calculations and can return through inverse process can be a highly valuable support for higher level statistics – particularly comprehension of aspects of standard deviation.
The formula for standard deviation is structurally similar to that of Pythagoras’ Theorem – this allows emphasis for the requirement for the interpretation of a standard deviation value to include the appropriate measurement units of the collected data within a sample. Given the fact that variance is the squared value of SD, this builds a justification as to why variance (as a squared unit) would not have a logical unit for direct representation and linking to the mean (for outlier identification/interpretation of results), whereas standard deviation does.
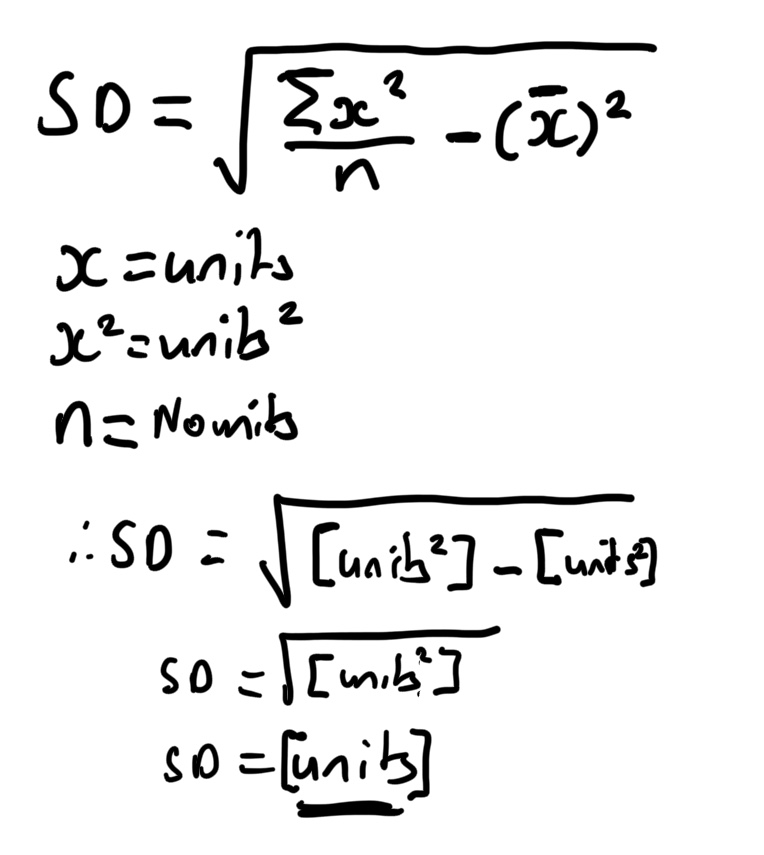
Concepts of algebra such as ‘like terms’ also have interlinked mathematical underpinning with dimensional analysis. Why can’t you add values of different units? (Can only collect like terms). Why do I have to convert units in order to get appropriate solutions? Whilst these decisions are often, again, discussed under the pretence of geometry and logic – these can also be illustrated with units as part of a calculation – and algebraic reasoning employed. It also provides an element of ‘real life’ pinning to basic algebraic methods beyond ‘apples and bananas’ style concepts often employed.

Understanding how units embed within calculations can also act as a support for unit conversion, particularly when spanning multiple dimensions, or converting a component element of a larger calculation – and a segue into substitution as the most effective algebraic method of simultaneous equations.


For me, having knowledge of units as mathematical artefacts, with the ability to apply this knowledge to your work is a highly desirable/essential need for a budding STEM student. What concerns me, is that at this moment in time, there is little to no formal emphasis on developing this trait throughout schooling in mathematics. So why is that the case?
A lack of bigger picture in the Maths curriculum
In some ways how students see the key stage 4 maths curriculum can be viewed like Channel 4 and Challenge TV favourite, “The Crystal Maze”. The syllabus is separated off into a variety of zones; algebra, number, geometry and measure, statistics etc, all with different sub-topics, of individual puzzles housed within them. A contestant in “The Crystal Maze” enters a room and meets a brand new puzzle that is unconnected to a previous problem, working their way through before moving on to another seemingly unconnected problem. Students often visualise the curriculum in a similar way and interact with it as such, particularly towards the end of their schooling due to the fragmented ‘individual puzzle’ nature of how GCSE maths exam questions are presented. Not only can it be incredibly rare for the different ‘zones’ to interact with each other (which is why situations like the “Hannah’s sweets” cause carnage), but also methods and topics inside them often sit nice and neatly compartmentalised, like the rooms of “The Crystal Maze”.

I was once in some training where during a discussion on assessment, a well respected maths colleague exclaimed “GCSE Maths doesn’t have assessment objectives, we have topic areas instead”. This was an incorrect observation, however it genuinely didn’t surprise me how even an experienced and very good maths teacher who has been brought through a KS4/KS5 system that is built on ‘exam focus’, could actually believe that. For reference, the first mention of ‘Assessment Objectives’ appears on page 9/26 of the AQA GCSE English Language specification, yet it is not until page 37/44 that they arise for GCSE Maths. Contrast this to the first mention of the content category mapping (number/algebra/geometry etc.), which is on page 7/44 – and makes up the largest portion of the whole document, you can soon see where the emphasis is placed.
Now, obviously content is always ‘king’, however in maths (and Science disciplines) the AO’s are essentially vessels to assess content. Unlike essay driven subjects, Maths and Science disciplines will tend to have larger percentage of content on the specification assessed in an exam. By contrast, essay driven disciplines are likely to have less content assessed, and it is such that the content then becomes the vessel to inform judgement on the assessment objectives.
With mathematics this approach leads to an overly concentrated focus onto the individual snippets of content – and not how all of these concepts and skills interact. In a recent blog post Daisy Christodolou discusses an interesting aspect with regards the national curriculum – such that ‘assessment’ is a much bigger driver of influence that the ‘national curriculum’ itself. When people say “this should be on the curriculum”, it’s rather shorthand for “students should be able to do this” and assessment is the mechanism in order to evidence this. Looking through this lens, the assessment at key stage 4 is the anathema to developing holistic meaning in mathematics – and despite the intentions of specific teachers, young people with the pressures of the current exam structure with the scattered snippets of content will always retreat to narrow content focus – as that is how they are rewarded.
Dimensional Analysis as a threshold concept
In chapter 7 of the fantastic “What if everything you knew about education was wrong?”, David Didau (2016) discusses the idea of disciplinary ‘threshold concepts’. These are defined beyond other accepted terminology such as ‘key concepts’ of a discipline. Instead threshold concepts possess wider qualities such as being transformative of your ability to engage with a subject, are irreversible, they reconstruct your knowledge and once they have been learned they are integrative, in that they likely allow you to make connections to different parts of a subject that you hadn’t previously seen as connected.
An educational theory that is gaining traction in higher education, but it is not something I have seen widely shared beyond that. The theory was first posited by academics, Jan H.F Meyer and Ray Land – huge amounts of information on their work and what follows can be found at the following site – https://www.ee.ucl.ac.uk/~mflanaga/thresholds.html. Land and Meyer define these concepts as akin to ‘conceptual gateways’ – which open up new ways of thinking within a discipline. The pair have curated a collection of essays, alongside Michael T. Flanagan entitled “Threshold Concepts in Practice” which was published in 2016 – this includes a number of disciplines such as engineering, medicine, nursing, computer science, law, architecture and teaching where frameworks and identification of threshold concepts have been attempted. Although, there is a significant HE focus to the work. However, just like how educators at all levels look to identify common pitfalls and misconceptions that students have to strategise for them appropriately, should we not also be looking to identify these transformational concepts in our curriculum?
With that in mind, viewing mathematics, particularly higher mathematics, its purpose as a catalyst in various progression routes in a range of disciplines – I feel as though a strong argument can be made for dimensional analysis to embed that “Unit symbols are mathematical entities and not abbreviations” as a fundamental threshold concept. It is transformative of approach in how it allows students to understand formulae and how variables can interact, it can be used to reconstruct knowledge of measurements and formulae – adaptable across a range of scientific disciplines. There are very clear connections that can be made across a range of different mathematical areas – that stem from passing through the conceptual gateway.
Now I haven’t mapped this fully to the generally accepted 8 features of a ‘threshold concept’ – which are; transformative, troublesome, irreversible, integrative, bounded, discursive, reconstructive and liminality. This is in part due to still wading my way through “Threshold Concepts in Practice” and a variety of other academic resources on the topic – however in my early reading and attempts of mapping to my discipline, this was something that jumped out immediately. When you teach a student that this ‘clicks’ for – you know – their ability to grasp and understand the formulae they work with – why calculations work, interpret graphs and ultimately transition into methods of calculus with far greater ease than their peers. I think you’d be hard pressed to find anyone involved in STEM and teaching of the sciences who doesn’t think this appreciation of measurement is an essential part of a young person’s development in a maths rich discipline, yet within the current curriculum constructs it is something that students are expected to essentially ‘accidentally stumble upon’, with no assessment incentive at earlier stages to embed this explicitly.
STEM based T Levels were some of the first launched reform qualifications at KS5, with engineering disciplines, health courses and lab science being key T Levels the government are wishing to recruit for. Interestingly these also make up the courses of the first wave of Alternative Academic Qualifications to be shortly launched – suggesting a demand in these areas that A Levels and T Levels alone cannot suffice, leading to a bevy of ‘more accessible’ L3 courses also need to be on offer in order to facilitate demand.
A 2023 report from the Campaign for Science and Engineering (CaSE) shares that the UK Government predicts at least 150,000 further researchers and technicians by the end of the decade, with the Institute of Engineering Technology (IET) going further to suggest a shortfall of 173,000 within the STEM sector. However, there is a disjointed approach to how curriculum has been structured – we aren’t supporting a diverse range of young people to pursue these courses due to reforms and changes to assessment at lower levels. Elements such as dimensional analysis, whilst not the most glamorous topic in the world, is a method that can both support and underpin abstract elements in the word ‘bubble of mathematics’, but also provide physical world application – the type of ‘real life maths’ a certain cross-section of the public clamour for.
There is so much more to units of measure than what we currently investigate within lower stage maths curriculum, and in my opinion, if we are wanting to encourage young people towards STEM rich disciplines, with labour market shortages – this is one very small area (of many) we should look to develop further to help build meaning in the eyes of the young people we teach.
REFERENCES & WIDER READING
Campaign for Science and Engineering (2023). The Skills Opportunity: Building a more innovative UK – https://www.sciencecampaign.org.uk/app/uploads/2023/06/CaSE-The-Skills-Opportunity-Report-June-2023.pdf
Christodolou, D (2024). Why the national curriculum is not as important as you think – https://substack.nomoremarking.com/p/why-the-national-curriculum-is-not
Didau, D (2016). What if everything we knew about education was wrong?. Crown House Publishing.
Land, R, Meyer, JHF & Flanagan, MT (2016). Threshold Concepts in Practice. Educational Futures: Rethinking Theory and Practice, volume 68. Sense Publishers.
Introduction and Bibliography of writing on Threshold Concepts – https://www.ee.ucl.ac.uk/~mflanaga/thresholds.html
Sherwood, J (2019). What can we learn from the 2019 GCSE Mathematics papers? – https://educationblog.oup.com/secondary/maths/exam-insights-gcse-maths

